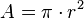Conclusión 

 Es muy importante en nuestra vida, ya que estudiándola podemos verla a través de ruedas de los automóviles, en los discos, construcciones con forma de circunferencia, entre otros; además que el estudiar la circunferencia mantiene nuestras mentes ágiles para poder tomar decisiones.

 Aplicar problemas que le sean familiares e interesantes. Se trata de que en cada uno de los subtemas participe proponiendo sus propios ejemplo y que sobre todo al final de la unidad él tenga la habilidad, confianza e iniciativa para inferir posibles soluciones. Dependiendo del área de interés al estudiante puede transportar dichos conocimientos, de tal manera que le auxilien para entender y resolver otro tipo de problemas. Pero hay tantas formas de resolver un problema por medio de un programa como alumnos distintos tenga un maestro.

CIRCUNFERENCIA CON CENRO (h,k) 

 En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (h,k) distinto del origen y radio r consta de todos los puntos (x, y) que satisfacen la ecuación.

 (x-h)² + (y-k)² =r², donde (h,k) es el centro y r es el radio.

 Para determinar la ecuación ordinaria de la circunferencia se necesita las coordenadas del centro y la medida del radio.

CIRCUNFERENCIA CON CENTRO (0,0)

Cuando el centro esta en el origen (0,0), La ecuación de una circunferencia se simplifica a :

A esta ecuación se le conoce como ecuación canónica y se da cuando el centro de la circunferencia es el punto c(0,0), por lo que la expresión ordinaria queda reducida a:  

Área del circulo delimitado por una circunferencia

 El área del círculo delimitado por la circunferencia es:

 Área del círculo = π × área del cuadrado sombreado.